About me
I am a second-year Ph.D. student in the Yale Graphics Group, performing computer graphics research under Dr. Theodore Kim. I recieved my B.S. in Computer Science from Yale in 2024. My research interests include geometry processing, fractal geometry and physical simulation. I was selected as a runner-up for the 2024 CRA Outstanding Undergraduate Researcher Award.
Publications

We present a novel, directable method for introducing
fractal self-similarity into
arbitrary shapes. Our method allows a
user to directly specify the locations
of self-similarities in a Julia set and is
general enough to reproduce other
well-known fractals such as the Koch snowflake.
Ours is the first algorithm to enable this level of general artistic control while also maintaining the character of the original fractal shape. We introduce the notion of placing “portals” into the iteration space of a dynamical system, bridging the aesthetics of iterated maps with the fine-grained control of iterated function systems (IFS). Our method is effective in both 2D and 3D.
Ours is the first algorithm to enable this level of general artistic control while also maintaining the character of the original fractal shape. We introduce the notion of placing “portals” into the iteration space of a dynamical system, bridging the aesthetics of iterated maps with the fine-grained control of iterated function systems (IFS). Our method is effective in both 2D and 3D.

We present an efficient new method for computing Mandelbrot-like fractals (Julia sets) that approximate a user-defined shape.
Our algorithm is orders of magnitude faster than previous methods, as it entirely sidesteps the need for a time-consuming numerical optimization.
It is also more robust, succeeding on shapes where previous approaches failed.
The key to our approach is a versor-modulus analysis of iterated function systems that allows us to formulate a novel shape modulus function that directly controls the broad shape of a Julia set, while keeping fine-grained fractal details intact.
Our formulation contains flexible artistic controls that allow users to seamlessly add fractal detail to desired spatial regions, while transitioning back to the original shape in others. No previous approach allows these sort of Mandelbrot-like details to be "painted" onto meshes.
The key to our approach is a versor-modulus analysis of iterated function systems that allows us to formulate a novel shape modulus function that directly controls the broad shape of a Julia set, while keeping fine-grained fractal details intact.
Our formulation contains flexible artistic controls that allow users to seamlessly add fractal detail to desired spatial regions, while transitioning back to the original shape in others. No previous approach allows these sort of Mandelbrot-like details to be "painted" onto meshes.
Talks



Other Projects
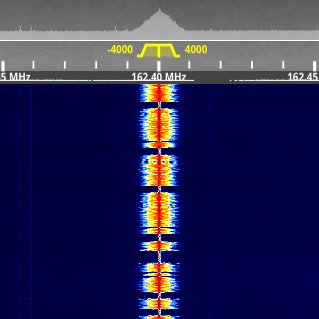
I operate an OpenWebRX+
instance located in downtown New Haven consisting of a
RTL-SDR tuner connected to a 2 meter dipole
antenna. The interface supports client-side decoding of
AM/FM/SSB, DMR, APRS, Fax, SSTV, CW, and a large number
of other protocols. You can right-click the tuning
arrows to change the SDR's center frequency.
The SDR should be available 24/7, except for when I am making radio transmissions, during which I disconnect the SDR's antenna to prevent damage.
The SDR should be available 24/7, except for when I am making radio transmissions, during which I disconnect the SDR's antenna to prevent damage.
